Today, we will learn about scatter plots, which are simple plots giving us insights into trends of the data. We will go deeper with some advanced features that make scatter plots an invaluable gift for effective data visualization.
What is a Scatter Plot?
Scatter plots are commonly use in statistical analysis in order to visualize numerical relationships. They are use in order to compare multiple measures by plotting them on the x and y-axis. hence, Let us look at a case study about cell phone brands and their ratings, reviews, and prices.
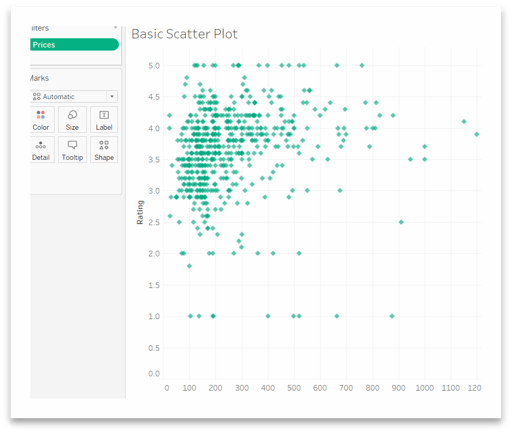
Figure 1 – Scatter Plot
Useful Links – CBDA Certification Training Course, | Tableau Certification program, | Power BI certification program, | Data Analytics Fundamentals Course
So, we can look at Figure 1 and understand that we can get good cell phones at lower prices. Most of the points are concentrate in low price ranges and ratings above 3. We can see a weak relation of prices increasing as rating increases.
Identifying Correlations using Trend Lines
Scatter plots are used in order to determine whether two measures are correlated. Let us see how they help us understand the strength of correlation of the two measures. For instance, In a linear correlation, the plotted points form a straight line. It can be positive or negative.
Strong Linear Correlation – All points are tightly packed around the straight line. Diagram reference
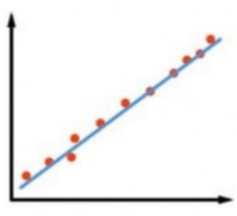
y co-ordinate also increases. Points are packed near the line.
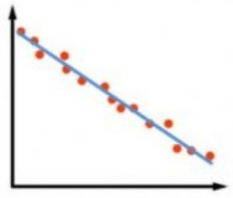
Weak Linear Correlation – Points are very loosely packed around the straight line.
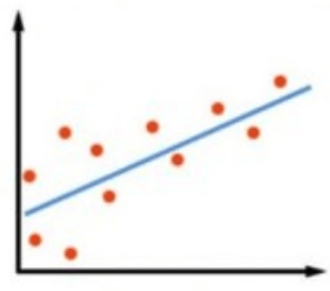
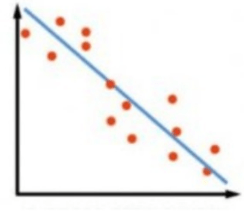
The line passing through the points is naming a trend line which shows the correlation of variables. A trend line is an equation that shows the relationship between measures. Such that it is the best fit for the data. They indicate how strong or weak the relationship is and if any outliers are affecting the trend line. They give us the p-value and R-squared values, which tell us how well our line is fitting to the data. As a general rule, a low p-value usually less than 0.005 and an R-squared value closer to 1 signifies a good model.
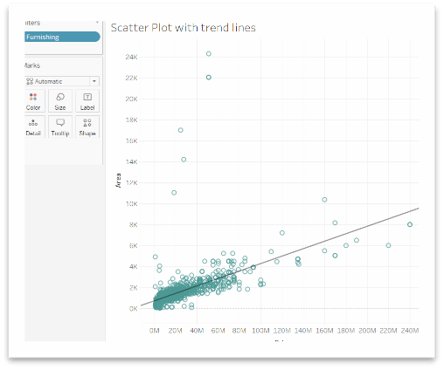
For instance, let us look at a use case with a data set containing different dimensions like furnishing – furnished or unfurnished, locality, status – ready to move or almost ready, transaction – New or resale, type – apartment or builder floor (entire floor for the occupant), per square feet price and price. So, We will plot a scatter plot of two measures – area against price and the trend lines for both.
Case Scenario
- Here, we can see from Figure 2 that data points are concentrate in the lower price and lower area range.
- We have drawn a linear trend line in which both variables that transforms by the natural logarithm ln(Y), ln(X) before the model is estimate. It has a p-value less than 0.0001 and R-squared 0.33, indicating that this might not be the best model.
- We can try different trend line models provided by Tableau. It is like logarithmic, power, polynomial, etc.
- A few outliers are indicating larger area houses available for lower prices.
Know more about our CBDA Certification Training Course, Tableau Certification program, Power BI certification program, Data Analytics Fundamentals Course
Trend Lines with Discrete Dimension
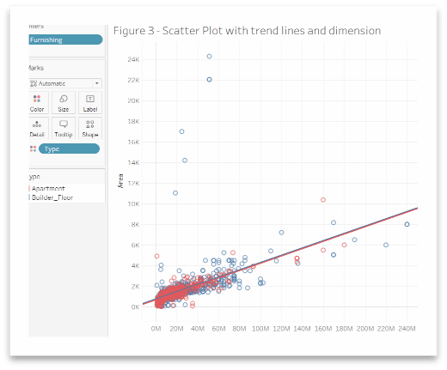
We can add a discrete dimension to differentiate the points plotted and compare the differences. For instance, We have added Type in the color marks and plotted the linear trend line for both Types – Apartment and Builder Floor.
We can see that the points are color based on the Type, and both have almost the same linear trend lines.
Scatter Plots with Reference Lines
Reference lines help us to identify segments in the data set. For example, if we add reference lines for average values of rating and prices in Figure 1, we will get four quadrants, as shown in Figure 4.
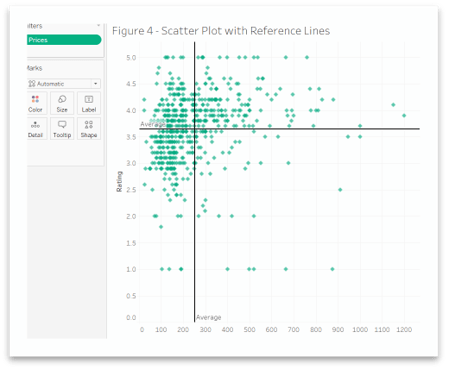
We can easily identify that there is more concentration of points in Q2 and Q3, indicating that most cell phones are available for lower prices. We also have few cell phones in Q1 indicating that high-end phones with higher costs have more user satisfaction.
Scatter Plot with Parameters
Using this feature of Tableau, we can give the user the control to select the second measure to compare with the fixed price measure. This also prevents the creation of multiple scatter plots.
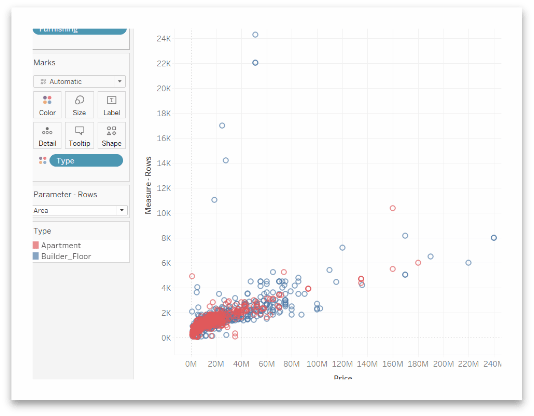
We can see the Parameter – Rows and we can select area, bathroom, BHK, and parking from the drop-down list to be compare with price.
Scatter Plot with Clusters
This is an advanced feature, using which we can divide the points into groups using an algorithm. Closer points are groupe in one cluster, while distant data points are separate in different clusters. They can be in any shape or form and help us draw valuable information about the data trends.
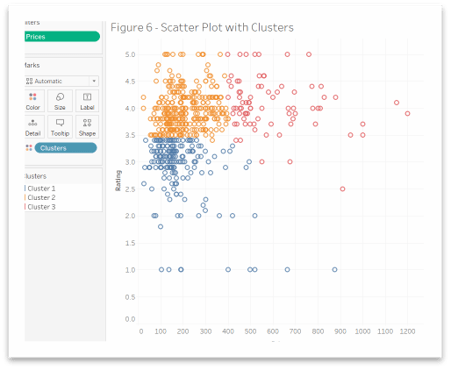
Figure 6 shows three different color-coded clusters giving us an immediate idea that cluster 2. (low price, high rating) in orange color is most dense and tightly packed. Cluster 1 in blue color has more outliers as compared with cluster 3. Customers prefer getting lower-price but good-performance cell phones, while fewer customers are looking for high-end and high-priced cell phones. Some customers want cheaper cell phones even if they don’t have great performance.
Uses and Pitfalls of Scatter Plots
- Use when you want to find out the correlation between two numerical variables/measures.
- Suitable to identify a linear or non-linear relationship in the data.
- Used when you want to look at the exact data points in your data. Minimum and maximum values, and identify clusters.
- Looking at the past trend can help us predict future values of a measure. It is based on the other measure we have plotted.
- Avoid a scatter plot when you have too much data, as it will cause overlapping and make the graph confusing.
- Being aware of interpreting correlation as causation. Even if we observe a relationship between two variables in a scatter plot. it does not mean that changes in one variable will be responsible for changes in the other variable. It might be possible that the observed relationship is due to a third factor, or may it is just a coincidence.
Conclusion
For instance, We learned a great deal about scatter plots and different tools to help us interpret them. It’s like trend lines, reference lines, and clusters. So, Good exposure to business and more practice interpreting scatter plots will help us understand them in more detail. You can also read our latest blogs related to Data Visualization, Creating Good Visuals Using Tableau, and many more…